线性相关与线性无关

线性无关(Linearly Independent)，指一组向量中，任一向量都不能通过其他向量的线性组合得到，那么就称这些向量是“线性无关”的。

在进一步探讨线性无关之前，我们先来了解一下，什么是线性相关？

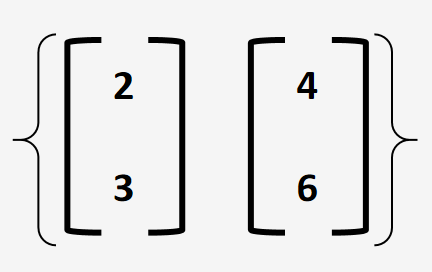
设有如下2个向量，它们所张成的空间是什么？

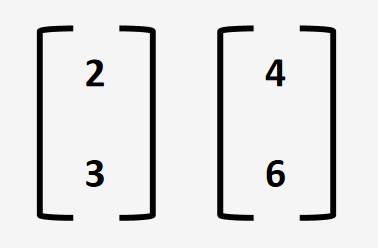
一个常数乘以一个向量加上另一个常数乘以另一个向量

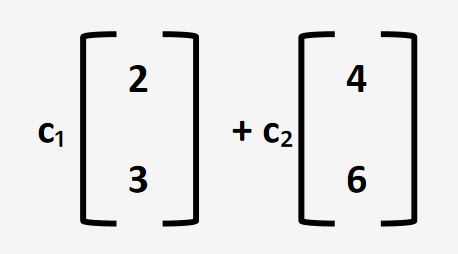
当我们给c1、c2赋予实数值时，就得到了这2个向量所能表示的线性组合的向量的集合，即这2个向量的张成的空间。

你可能会发现，第二个向量可以通过第一个向量乘以2得到。

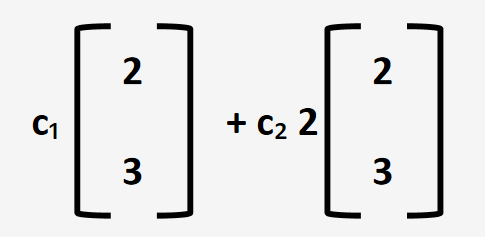
继续化简

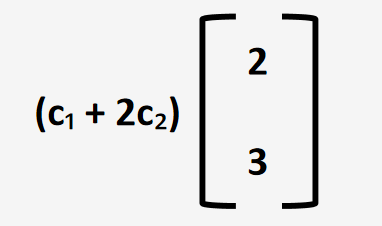
我们可以发现，两个向量的线性组合在化简后只剩下第一个向量，第二个向量(4,6)可以用第一个向量的2常数倍表示。那么我们可以说这个2个向量是线性相关的。当然我们也可以用第二个向量(4,6)的二分之一倍来表示第一个向量。

我们也可以通过图例来考察这个概念。

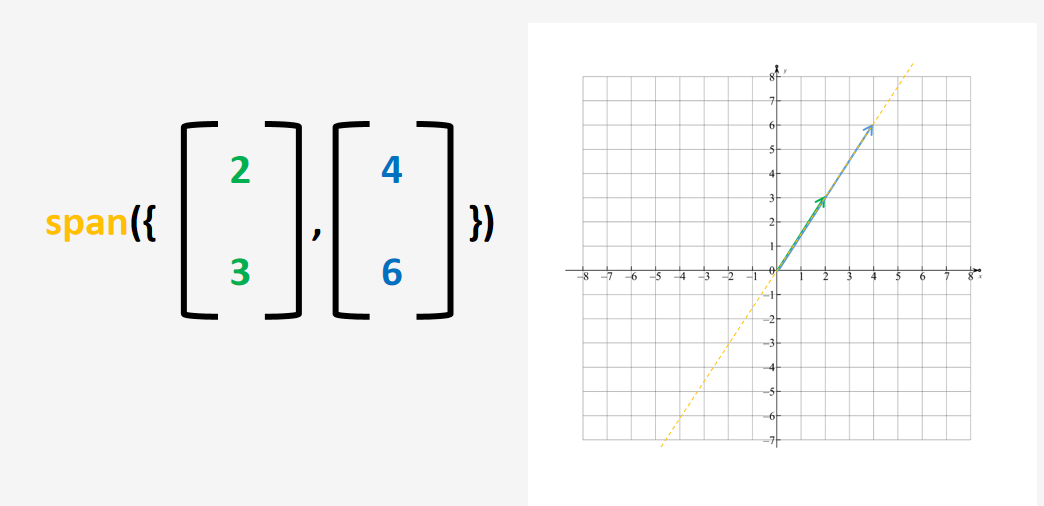
这2个向量张成的空间是一条直线，他们是共线的，二者是倍数关系，二者的线性组合无法表示出这条直线之外的向量。它们退化成了一个向量，那我们称这2个向量的集合是线性相关的。

线性相关意味着，集合中的一个向量可以由集合中的其他向量的组合表示而成。关于这个概念的一个考虑方式是不论你选择了什么向量都不会新增定向或者其他信息。比如集合中已存在了向量(2,3)，当加入了向量(4,6)后，这个集合张成的空间规模并未扩大，仍然是在这条直线之上，未超出这条直线。

我们再举一个例子，下面这3个向量是线性相关的还是线性无关的呢？

其实你仔细观察一下，向量V1 加上 V2 的线性组合可以得到V3，

故向量V1、V2、V3是线性相关的。

从这里我们可以得到一个一般性的概念，即：已知二维空间中的三个向量，其中有一个一定是多余的。

接下来，我们再看看这个例子

我们无法将V1乘以某个标量得到V2，比如7×0得到0，但是0×0是无法得到-1，故我们称向量V1、V2是线性无关的，且V1、V2张成的空间等于R2,即 span(V₁ , V₂) = R²。

判断n个向量是否是线性相关的

那么有什么方法可以快速判断n个向量是否是线性相关或者线性无关的？

我们先给出一个定义：

在向量空间R的一组向量集合（如{V₁ , V₂ , V₃ , ... , Vₙ}），如果存在一系列“不全为零(或者是至少有一个不为零)”的数(如C₁ , C₂ , C₃ , ... , Cₙ)，使得 C₁V₁ + C₂V₂ + C₃V₃ + ... + CₙVₙ = 0 ，则称这个向量集合是线性相关的，否则(即C₁ , C₂ , C₃ , ... , Cₙ全为0时)这些向量是线性无关的。

我们尝试使用一个例子来说明，设有2个向量

代入上面的公式

进一步展开

根据向量加法，我们可以将其变成一个二元一次方程组

求解，我们得到

而根据定义可得，这2个向量是线性无关的。

我们再举另外一个例子，有一个向量集合，里面有3个向量，他们是线性相关的，还是线性无关的呢？

代入上面的公式

我们得到一个三元一次方程组

求解，得到

我们代入任意非0的常量t都可以得到一组至少有1个不为0的数，比如代入1，就可以得到 4，-3， 1。而根据上面的定义，我们就可以说这几个向量是线性相关的。

定义的推导

下面我们尝试推导出这个定义，其实很简单，如果某个向量与其他向量是线性相关的，那么它可以通过其他向量的线性组合得到，即

而在等式的两边都减去V₁后，我们得到

这里的-1即代表了定义中的：存在一系列“不全为零(或者是至少有一个不为零)”的数时。此时，这组向量是线性相关，反之，即线性无关的。